MATLAB练习记录册
期末复习
选择题
1.1
所用函数的输出变量数目的特殊变量
nargout
1. 变量的命名规则
- § 变量名区分字母的大小写。例如,“a”和“A”是不同的变量。
- § 变量名不能超过63个字符,第63个字符后的字符被忽略,对于MATLAB6.5版以前的变量名不能超过31个字符。
- § 变量名必须以字母开头,变量名的组成可以是任意字母、数字或者下划线,但不能含有空格和标点符号(如,。%等)。例如,“6ABC”、“AB%C”都是不合法的变量名。
- § 关键字(如if、while等)不能作为变量名。
2. 特殊变量
MATLAB有一些自己的特殊变量,当MATLAB启动时驻留在内存。
表2.1 特殊变量表
| 特殊变量 | 取值 |
|---|---|
| ans | 运算结果的默认变量名 |
| pi | 圆周率π |
| eps | 计算机的最小数 |
| flops | 浮点运算数 |
| inf | 无穷大,如1/0 |
| NaN或nan | 非数,如0/0、∞/∞、0×∞ |
| i或 j | i=j= |
| nargin | 函数的输入变量数目 |
| nargout | 函数的输出变量数目 |
| realmin | 最小的可用正实数 |
| realmax | 最大的可用正实数 |
l 在MATLAB中系统将计算的结果自动赋给名为“ans”的变量。
2*pi
ans =
6.2832
1.2
Matlab的关系运算符
关系运算符是指两数值或字符操作数之间的运算符,这种运算将根椐两操作数的关系产生结果 true 或 false。
MATLAB 中的关系运算符有 6 个,如下表所示:
| 关系运算符 | 描述 |
|---|---|
| < | 小于 |
| <= | 小于或等于 |
| > | 大于 |
| >= | 大于或等于 |
| == | 等于(请不要和赋值等号 = 混淆) |
| ~= | 不等于 |
1.3
1 | |
1 | |
1.4
1 | |
1 | |
1.5
在[0,2]区间绘制$y=x^2sinx$的图形程序
1 | |
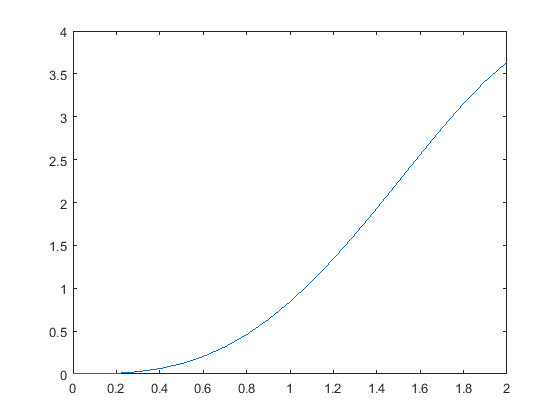
1. 算术运算
MATLAB的算术运算是在矩阵意义下进行的,单个数据的算术运算只是矩阵运算的一种特例
| + | 加 |
|---|---|
| - | 减 |
| * | 乘 |
| / | 右除 |
| \ | 左除 |
| ^ | 乘方 |
① 加减运算
若两矩阵同型,则运算时两矩阵的相应元素相加减
若两矩阵不同型,则MATLAB将给出错误信息
一个标量和矩阵进行加减运算,则标量和矩阵的每一个元素进行加减运算
② 乘法运算
矩阵A和B进行乘法运算,要求A的列数与B的行数相等
如果两者的维数或大小不相容,则将给出错误信息
③ 除法运算
两种矩阵除法运算:右除/和左除\
A矩阵是非奇异方阵,则B/A等效于B*inv(A),A\B等效于inv(A)*B
④ 乘方运算
矩阵的乘方运算可以表示成A^x,要求A为方阵,x为标量
⑤ 点运算
点运算符
| .* | ./ | .\ | .^ |
|---|---|---|---|
两矩阵对应元素进行相关运算,要求两矩阵同型或其一(被除)为标量
1 | |
2. 关系运算
关系运算符
| < | <= | > | >= | == | ~= |
|---|---|---|---|---|---|
两标量进行比较,直接比较两数大小,真为1,假为0
两个同型矩阵比较,相应位置逐一比较,结果是同型矩阵,相应位置真为1,假为0
e.g. 判断A的元素是否为偶数
1 | |
3. 逻辑运算
| &(与) | |(或) | ~(非) |
|---|---|---|
① 运算规则
设a和b为标量
a&ba、b,全为非零时,运算结果为1,否则为0
a|ba、b,中只要有一个为非零时,运算结果为1
~a,当a为零时,结果为1;当a为非零时,结果为0
② 参与逻辑运算的是两个同型矩阵,那么对应位置逐一运算,结果为同型矩阵,其元素由1或0组成
③ 若参与逻辑运算的一个是标量,一个是矩阵,那么将在标量与矩阵中每个元素都进行运算,结果为同型矩阵,其元素由1或0组成
e.g. 水仙花数是指各位数字的立方之和等于该数本身的三位正整数
1 | |
matlab 语法积累-点乘是对应元素相乘 乘是行乘列
第一步我们首先需要知道,如果a和b是两个矩阵的话,a*b是进行矩阵相乘,a.*b是a矩阵的每一个元素乘以b矩阵对应位置的元素形成的一个新矩阵,一般两个矩阵运算使用点乘,如下图所示:
In the first step, we first need to know that if a and b are two matrices, a*b is a matrix multiplication, and a.*b is a new matrix formed by multiplying each element of the a matrix by the element at the corresponding position of the b matrix. Matrix, generally two matrix operations use dot product, as shown in the following figure:
matlab中点乘与乘的区别
乘是矩阵的运算,点乘是矩阵中元素的运算。
a*b表示矩阵a与矩阵b进行矩阵相乘。
a.*b表示矩阵a中的元素与矩阵b中的元素按照相同位置进行相乘,
得到的结果作为新矩阵中相同位置的元素。
第二步我们来看一下例子,在matlab命令行窗口中输入a=[1 2;2 4],b=[1 5;3 6],创建a和b两个矩阵,如下图所示:
In the second step, let’s take a look at the example, enter a=[1 2;2 4], b=[1 5;3 6] in the matlab command line window to create two matrices a and b, as shown in the following figure:
1 | |
第三步在命令行窗口中输入a*b,可以看到是两个矩阵相乘的结果,如下图所示:
The third step is to enter a*b in the command line window, and you can see that it is the result of multiplying two matrices, as shown in the following figure:
1 | |
第四步输入a.*b,按回车键之后,可以看到是两个矩阵每个对应位置元素相乘形成的一个新矩阵,如下图所示:
The fourth step is to enter a.*b, and after pressing the Enter key, you can see that it is a new matrix formed by multiplying each of the corresponding position elements of the two matrices, as shown in the following figure:
1 | |
第五步最后我们可以看一下矩阵乘以数值的结果,也是每个元素乘以数值形成的新矩阵,矩阵乘数值和矩阵点乘数值的结果是一样的,如下图所示:
Step 5 Finally, we can look at the result of multiplying the matrix by the value, which is also a new matrix formed by multiplying each element by the value. The result of the matrix multiplier value and the matrix point multiplier value is the same, as shown in the following figure:
1 | |
矩阵与数的“点乘”结果与矩阵乘以数的结果相同。
The result of “dot multiplication” between a matrix and a number is as same as the result of multiplying a matrix by a number.
1 | |
1.6
绘制$r=4sin(5x)$的极坐标图形程序:
1 | |
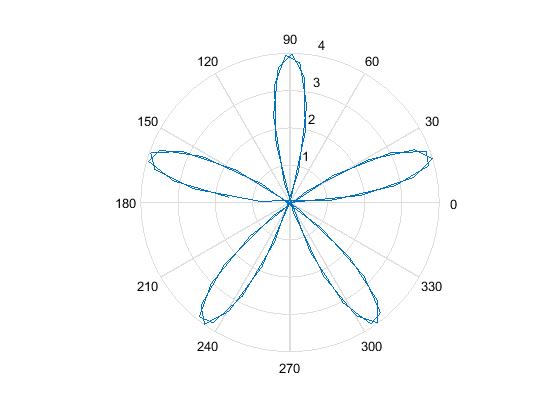
polar可用于描绘极坐标图像。
最简单而经常使用的命令格式:POLAR(THETA, RHO)
当中,THETA是用弧度制表示的角度,RHO是相应的半径。
例:
1 | |
得到
这也是传说中笛卡尔最后一封情书中蕴含的秘密
借这个曲线献给爱的这个·世界和你
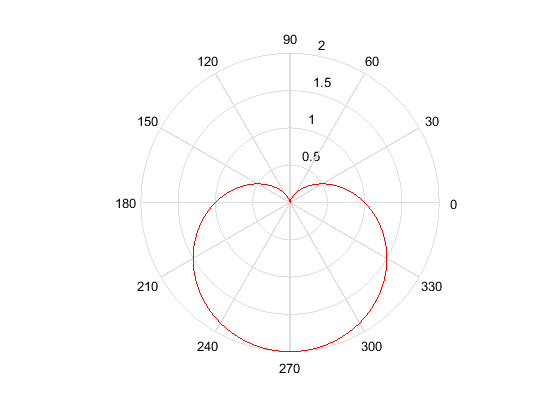
1.7
1 | |
此处注意,如果加了分号的话,就不直接显示输出了呢。
1 | |
参考翻译
帮助诠释
— sym/int 的帮助 —整合
int(S) 是 S 关于其符号的不定积分
由 SYMVAR 定义的变量。 S 是一个 SYM(矩阵或标量)。
如果 S 是常数,则积分是关于“x”的。int(S,v) 是 S 关于 v 的不定积分。v 是 标量 SYM。 int(S,a,b) 是 S 关于它的定积分 从 a 到 b 的符号变量。 a 和 b 都是双精度或 符号标量。也可以指定积分间隔 使用具有两个元素的行或列向量,即有效 调用也是 int(S,[a,b]) 或 int(S,[a b]) 和 int(S,[a;b])。 int(S,v,a,b) 是 S 关于 v 的定积分 从a到b。也可以指定积分间隔 使用具有两个元素的行或列向量,即有效 调用也是 int(S,v,[a,b]) 或 int(S,v,[a b]) 和 整数(S,v,[a;b])。 int(...,'IgnoreAnalyticConstraints',VAL) 控制的级别 用于分析约束的数学严谨性 解决方案(分支切割,除以零等)。的选项 VAL 为真或假。指定 TRUE 以放宽 求积分的数学严谨性。默认值为假。 int(...,'IgnoreSpecialCases',VAL) 控制答案的详细程度 是关于特殊参数值/选项的 VAL 为真或假。指定 TRUE 以忽略特殊情况 参数值。默认值为假。 int(...,'PrincipalValue',VAL) 用于请求 Cauchy 主体 定积分的值。 (无限期忽略该选项 积分。) VAL 的可能值为 TRUE 和 FALSE, 默认为假。 int 的其他函数命名
首先,调用格式
1 | |
现在我们来练一个简单的
求${\int \frac{-2x}{(1+x^2)^2} dx}$ 的不定积分
命令行输入
1 | |
运行得到
1 | |
So easy!
那我们现在换一个稍微难一点的
求 $\iint xe^{-xy} dxdy$ 的二重积分
命令行输入
1 | |
运行得到
1 | |
Still, so easy!
好嘞,那么我们现在换一个数值积分求一求玩玩咯
调用格式如下
1 | |
实战一下,计算$q=\int_{0}^{2} \frac{1}{x^3-2x-5} dx$ 的积分
命令行输入
1 | |
运行得到
1 | |
再来试一个梯形法
计算x在0~Π范围内,间隔为Π/100的sin(x)的数值积分,即:$z=\int_{0}^{\Pi } sin(x)dx$
命令行输入
1 | |
运行得到
1 | |
1.8
1 | |
1 | |
原文链接:
4.4 数值求导与积分
在数学计算中,积分和求导是最常见的运算。
4.4.1 导数与梯度
导数的数值计算是数值计算的基本操作之一。如牛顿法求根、微分方程求解、泰勒级数展开等,都离不开导数。
1.导数
在MATLAB中,diff函数被用来计算数值差分或者符号导数。本小节只介绍diff函数如何用来计算差分,符号导数的计算将在下一章介绍。
diff函数的调用语法如下。
(1)Y = diff(X):求X相邻行元素之间的一阶差分。
(2)Y = diff(X,n):求X相邻行元素之间的n阶差分。
(3)Y = diff(X,n,dim):在dim指定维上求X相邻行元素之间的n阶差分。
【例4-31】 diff函数应用示例。
1 | |
2.梯度
梯度也经常在数值计算中使用。MATLAB提供了gradient函数来进行梯度计算。gradient函数的调用语法如下。
(1)FX = gradient(F):返回F的一维数值梯度,F是一个向量。
(2)[FX,FY] = gradient(F):返回二维数值梯度的x和y部分,F是一个矩阵。
(3)[FX,FY,FZ,…] = gradient(F):求高维矩阵F的数值梯度。
(4)[…] = gradient(F,h):h是一个标量,用于指定各个方向上点之间的间距。
(5)[…] = gradient(F,h1,h2,…):指定各个方向上的间距。
【例4-32】 梯度求解示例。
1 | |
运行以上命令,可以得到如图4-3所示的结果。
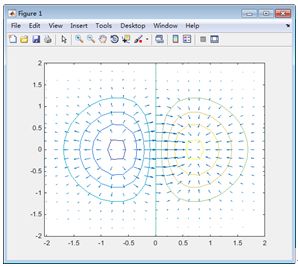
图4-3 梯度计算示例
4.4.2 一元函数的数值积分
1.quad函数
函数quad采用自适应Simpson方法计算积分,特点是精度较高,较为常用。quad函数的调用语法如下。
(1)q=quad(fun,a,b):计算函数fun在a到b区间内的数值积分,其中fun是一个函数句柄,默认误差为10-6。若给fun输入向量x,应返回y,即fun是一个单值函数。
(2)q=quad(fun,a,b,tol):用指定的绝对误差tol代替默认误差。tol越大,函数计算的次数越少,速度越快,但相应计算结果的精度会越低。
(3)[q,fcnt]=quad(fun,a,b):计算函数fun的数值积分,同时返回函数计算的次数fcnt。
【例4-33】 使用quad函数求的数值积分。
为了求函数的积分,首先要在工作目录下建立函数文件,不妨命名为myfun.m,该函数文件的内容如下:
1 | |
函数文件的创建与使用,将在第6章介绍。在建立好函数文件之后,需要传递相应的函数句柄@myfun到quad函数,同时需要指定上下限。
1 | |
函数quadl采用自适应Lobatto方法计算积分,特点是精度较高,最为常用。quadl函数的主要调用语法如下。
(1)q=quadl(fun,a,b):计算函数fun在a到b区间内的数值积分,其中fun是一个函数句柄,误差为10-6。若给fun输入向量x,应返回y,即fun是一个单值函数。
(2)q=quadl(fun,a,b,tol):用指定的绝对误差tol代替默认误差。tol越大,函数计算的次数越少,速度越快,但相应计算结果的精度会越低。
【例4-34】 使用quadl函数求的数值积分。
本例在前例建立的myfun文件基础上进行计算。
1 | |
3.trapz函数
trapz函数使用梯形法进行积分,特点是速度快,但精度差。trapz函数的调用语法如下。
(1)T=trapz(y):用等距梯形法近似计算y的积分。若y是一个向量,则trapz(y)为y的积分;若y是一个矩阵,则trapz(y)为y的每一列的积分。
(2)trapz(x,y):用梯形法计算y在x点的积分。
(3)T=trapz(…,dim):沿着dim指定的维对y进行积分。若参量当中包含x,则应有length(x)=size(y,dim)。
【例4-35】 trapz函数使用示例。计算。
通过数学推导可知,的精确值为2。现在我们以trapz函数进行计算以对比结果。首先需要划分梯形法使用的均匀区间:
1 | |
4.cumtrapz函数
cumtrapz函数用于求累积的梯形数值积分,其调用语法如下。
(1)Z=cumtrapz(Y):通过梯形积分法计算单位步长时Y的累积积分值,若步长不是一个单位量,则算出的Z值还应该乘以步长。当Y为向量时,返回该向量的累积积分;若Y为矩阵,则返回该矩阵每列元素的累积积分。
(2)Z=cumtrapz(X,Y):采用梯形积分求Y对X的积分,注意X与Y的长度必须相等。
(3)Z=cumtrapz(X,Y,dim)或Z=cumtrapz(Y,dim):对Y的dim维求积分,X的长度必须等于size(Y,dim)。
【例4-36】 cumtrapz函数应用示例。
1 | |
4.4.3 二重积分的数值计算
二重积分的数值计算可由函数dblquad实现。dblquad函数有以下几种语法格式。
(1)q=dblquad(fun,xmin,xmax,ymin,ymax):调用函数quad在区域xmin≤x≤xmax, ymin≤y≤ymax上计算二元函数z=fun(x,y)的二重积分。函数fun需要满足条件:输入向量x、标量y,则f(x,y)必须返回一个用于积分的向量。
(2)q=dblquad(fun,xmin,xmax,ymin,ymax,tol):用指定的精度tol代替默认精度10-6,再进行计算。
(3)q=dblquad(fun,xmin,xmax,ymin,ymax,tol,method):用指定的计算方法method代替默认算法quad。method的取值有@quadl或用户指定的与命令quad和quadl有相同调用次序的函数句柄。
【例4-37】 应用dblquad函数求重积分示例。
首先在工作目录下建立一个M文件integrnd.m,该文件内容为:
1 | |
然后调用dblquad函数求重积分:
1 | |
4.4.4 三重积分的数值计算
MATLAB提供了triplequad函数来对三重积分进行数值计算。该函数的调用语法如下。
(1)q=triplequad(fun,xmin,xmax,ymin,ymax,zmin,zmax):调用函数quad在区域[xmin,xmax, ymin,ymax,zmin,zmax]上进行三重积分运算。fun参数是一个M文件函数或匿名函数的句柄。
(2)q=triplequad(fun,xmin,xmax,ymin,ymax,zmin,zmax,tol):用指定的精度tol代替默认精度10-6进行计算。
(3)q=triplequad(fun,xmin,xmax,ymin,ymax,zmin,zmax,tol,method):用指定的计算方法method代替默认算法quad。method的取值有@quadl或用户指定的与命令quad与quadl有相同调用次序的函数句柄。
【例4-38】 用triplequad函数求三重积分。
首先需要在工作目录下建立函数M文件integrnd3.m,该文件内容为:
1 | |
然后在命令窗口输入:
1 | |
1.9

敲公式好费劲,以后再说吧,,,
1 | |
1.10

1 | |
a选项报错
1 | |
b,c选项报错
1 | |
[基础向]MATLAB常微分方程的解法
L v L CUMTB数学建模 2019-10-23 18:00

MATLAB
常微分方程的解法
微分方程是模拟自然、生物、工程等现象的重要数学工具。国赛中也有很多与微分方程有关的题目,如2018A高温作业专用服装设计、2014A嫦娥三号软着陆轨道设计与控制策略、2010A储油罐的变位识别与罐容表标定等,都是求解微分方程的定解问题。
★ 符号解法 ★
一、命令详解
● y=dsolve(‘equation’, ’cond1, cond2, …‘, ‘var’);
求解常微分方程equation满足初值条件cond1, cond2, … 的解。
● S=dsolve(‘equation1’, ‘equation2’, …, ‘cond1’, ‘cond2’, …);
求解多个常微分方程equation1, eqution2, … 满足初值条件cond1, cond2, … 的解,并以结构体的形式输出。
注:常微分方程equation中,符号D表示对变量进行求导,D2,D3,…分别为二阶、三阶导数。
二、案例分析
例1:求解两点边值问题:
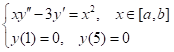
代码:
1 | |
★ 数值解法简介 ★
对于一些微分方程的定解问题,其解析解是不存在的或是难以求得的,因此,我们通常采用一些方法求得微分方程的数值解。所谓数值解,是指在求解区间内一系列离散点处给出真解的近似值。
微分方程和定解条件一起组成定解问题。定解条件通常有两种给法:
(1)初值问题(IVP):给出积分曲线初始时刻的状态;
(2)边值问题(BVP):给出积分曲线首末两端的状态。
对于一阶方程,往往只需要初值条件就可以得到方程的解;对于二阶或者二阶以上的微分方程,则可能需要边值条件。
★ 初值问题 ★
一、简介
一阶常微分方程的初值问题:
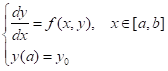
MATLAB提供了多个一阶常微分方程(组)初值问题数值解的函数,一般函数调用格式为:
● [t,y]=solver(fname,tspan,y0, [options]);
其中,t 和 y 分别给出了时间向量和状态向量;solver 为求解常微分方程数值解的函数,细节见下表;fname 为微分方程函数名;tspan 为指定的积分区间;y0 用于指定初值;option 用于改变计算中积分的特性(本文不详述)

二、案例分析
例2:一阶常微分初值问题:
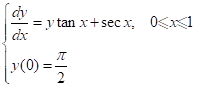
● 编写微分方程函数文件 fun1.m
1 | |
● 求解微分方程
1 | |
● 结果
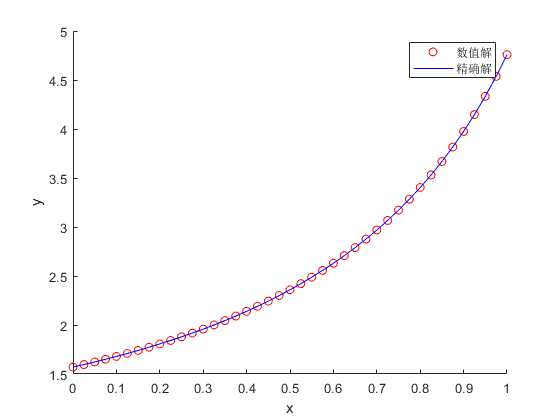
例3:二阶常微分方程初值问题:
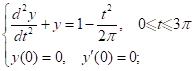
● 由于 ode23 和 ode45 都是对一阶常微分方程设计的,对于高阶微分方程,需要先将其转化为一阶常微分方程组,即状态转移方程。令 x1=y,x2=y’,则原方程的转化为:
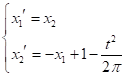
● 编写微分方程函数文件fun2.m
1 | |
● 求解微分方程组
1 | |
● 结果
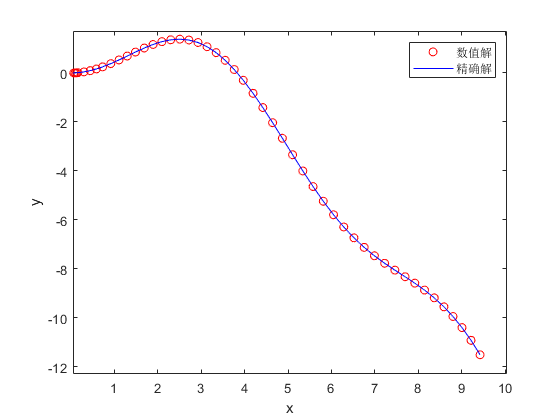
★ 边值问题 ★
一、命令详解
一阶常微分方程的初值问题:
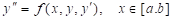
需要两个特定的条件,除了初值条件外,也可以通过给定边值条件来确定。边值条件一般有三种给定方法(这里不详细给出)。
二、基本命令
● solinit = bvpinit(x, yinit)
生成 BVP 求解器的所必须的初始估计值返回解结构体的初始估计值。x 指定边界区间[a,b]上的初始网格,要求x(1)=a,x(end)=b,点格要求单调;yinit是对解的初始猜测,指定为向量或函数。
● sol = bvp4c(odefun,bcfun,solinit)
求常微分方程的边界值问题的近似解,返回解结构体。odefun为要求解的函数,指定为函数句柄。bcfun为边界条件,指定为计算边界条件中残差的函数句柄。solinit为解的初始估计值,由函数bvpinit创建。
● y = deval(x, sol)
计算 x 中包含的点处的微分方程问题的解 sol。
三、案例分析
例4:考虑二阶常微分方程边值问题:
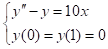
● 将高阶微分方程转化为一阶常微分方程组。令 y1=y,y2=y’,则原方程的转化为:
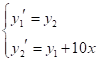
● 编写微分方程函数文件 odefun.m
1 | |
● 编写边界条件函数文件 bcfun.m
1 | |
● 求解微分方程组
1 | |
● 结果
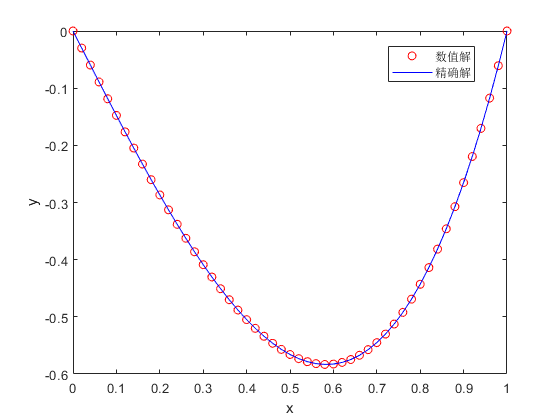
1.11
1 | |
MATLAB常用矩阵运算指令
15 人赞同了该文章
MATLAB中矩阵向量生成矩阵向量生成
MATLAB中矩阵向量生成常用三种方法:
[1]直接输入向量
x1=[1 2 4], x2=[1,2,4], x3=x1’
- 特别注意:这里x1和x2加不加逗号表示同一个向量
[2]冒号创建向量
x1=3.4:6.7,
x2=3.4:2:6.7,
- 特别注意输出结果x1=3.4 4.4 5.4 6.4 x2=3.4 5,4
[3]生成线性等分向量
常用指令x=linspace(a,b,n) 在[a,b]区间产生 n 个等分点(包括端点)
- 例如:x=linspace(0,1,5)
- 结果:x = 0 0.2500 0.5000 0.7500 1.0000x = 0 0.2500 0.5000 0.7500 1.0000
MATLAB中的矩阵运算
MATLAB中矩阵运算非常多,这里列出一些常用矩阵运算:中矩阵运算非常多,这里列出一些常用矩阵运算:
设三维向量x=[x1 x2 x3]; y=[y1 y2 y3]; ,a, b为标量。
- 向量的数乘:ax=[ax1 ax2 ax3]
- 向量的平移:x+b=[x1+b x2+b x3+b]
- 向量和:x+y=[x1+y1 x2+y2 x3+y3]
- 向量差:x-y=[x1-y1 x2-y2 x3-y3]
- 向量乘积:x.y=[x1y1 x2y2 x3y3]
- 向量右除:x./y=[x1/y1 x2/y2 x3/y3] (右边的y做分母)
- 向量左除:x.\y=[y1/x1 y2/x2 y3/x3] (左边的x做分母)
- 向量乘幂:x.^5=[x1^5 x2^5 x3^5]
- 2.^x=[2^x1 2^x2 2^x3]
- x.^y=[x1^y1 x2^y2 x3^y3]
MATLAB中特殊矩阵生成
MATLAB中其实有非常多特殊矩阵,用于数据初始化,方便矩阵运算等。这里也给出一些常用的特殊矩阵。中其实有非常多特殊矩阵,用于数据初始化,方便矩阵运算等。这里也给出一些常用的特殊矩阵。
全1阵:ones(n), ones(m,n), ones(size(A))
全零阵:zeros(n) ,zeros(m,n), zeros(size(A))
- 特别注意:全零阵常常用于对某个矩阵或向量赋0初值
- 单位阵:eye(n),eye(m,n)
- 随机阵:rand(m,n), rand(n)=rand(n,n)用于随机模拟,常和rand(‘seed’,k)配合使用。
MATLAB中常见矩阵函数
- det(A) :方阵的行列式;
- rank(A):矩阵的秩;
- eig(A):方阵的特征值和特征向量;
- trace(A):矩阵的迹;
- rref(A):初等变换阶梯化矩阵A
- svd(A):矩阵奇异值分解。
MATLAB中矩阵分析常用指令
MATLAB经常会涉及数据分析,MATLAB也提供了很多数据分析指令:
- 求最大值:max
- 求最小值:min
- 求平均值:mean
- 求和:sum
- 求标准差:std
- 求累积和:cumsum
- 求中值:median
- 求差分:diff
- 升序排列:sort
- 行升序排列:sortrows
当然其实MATLAB的函数远不止这些,这只是基础的矩阵运算。但是了解这些基础指令对你快速学习MATLAB会有很大帮助。MATLAB会有很大帮助。
编辑于 2021-04-24 23:42
1.12
solve函数常用于求解符号函数的解析解,方程组的解等
1.solve求解析解
1 | |
同样可以写成 solve(‘x+y=3’,’x’);
但是这样的话就没法给y赋值了,所以使用 subs函数
1 | |
2.solve解单变量方程
1 | |
这段代码的matlab运行结果是
1 | |
3.求解多变量方程
%如果不指明的话,solve函数就会通过symvar选择一个变量(认为该变量是要求解的变量)
1 | |
1.13
matlab的随机数生成函数总结!
在常见的编程语言中,比如C,python,等等,他们都有生成随机数的函数,或者是模块,当然,这里的随机应该是带引号的随机,准确的来说是伪随机,是基于一种算法而产生的数据,当然,这在平时的一些应用中是完全没问题的。
今天,咱们就聊一聊matlab中的随机函数。
1,rand(m,n)
含义:生成0-1间均匀分布的随机矩阵(m行,n列),如果m=n,则可简写为rand(m)
1 | |
2,randn(m,n)
含义:生成标准正态分布矩阵(m行,n列),如果m=n,则可简写为randn(m)
1 | |
3, a+(b-a)*rand(m,n)
含义:生成a-b间均匀分布的随机矩阵(m行,n列),如果m=n,则可简写。
1 | |
4,randi ([min,max],m,n)
含义:生成min到max之间的整数随机矩阵(m行,n列),如果m=n,则可简写为randi ([min,max],m)
1 | |
当然,上面的只是一些比较常见的函数而已,在平时的数学实验中比较常用,事实上,还有许多生成随机数的函数,在这里我就不一一列举了。
注:上面的均匀分布,正态分布在概率论中有明确的解释,当然,下次也会专门写一篇文章来分析一下。
最后,随机函数到底有什么用?其实在我看来,一个很重要的方面就是,在有些实验中,我们需要不确定的初值,同时减少人为因素的干扰,以接近实际状况的角度实验,看看初值对于实验结果的影响,以此来研究算法的稳定性等问题。
1.14
1 | |
1.15
1 | |
写程序
2.1
x=-6:0.1:6; —————————–2’
y=-14:0.1:14; —————————–2’
[x,y]=meshgrid(x,y); —————————–2’
z=x.^2-y.^2/4; —————————–2’
surf(x,y,z); —————————–2’
2.2
fun=@(x)[x(1)-x(2)+1,sin(x(1))-x(2)]; —————————–3’
x0=[-2 -1]; —————————–3’
[x,f,h]=fsolve(fun,x0); —————————–4’
2.3
X的一组样本[12.12 12.15 12.08 12.09 12.13 12.11 12.01 12.03 12.06],编写求总体均值 的置信区间的程序( =0.05)。
([mu,sig,muci,sigci]=normfit(x, ))
x=[12.12 12.15 12.08 12.09 12.13 12.11 12.01 12.03 12.06]; ——————–4’
[mu,sig,muci,sigci]=normfit(x,0.05); ——————————6’
2.4
syms x
a0=1/pi*int(x^2,x,-pi,pi);
ser=a0/2; —————————6’
for k=1:6
ak=1/piint(x^2cos(k*x),x,-pi,pi);
ser=ser+akcos(kx); —————————-4’
end
日常练习
1.5
指数螺旋曲线
1 | |
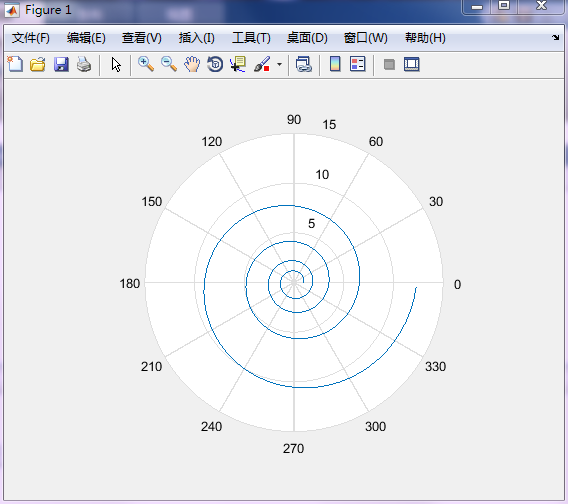
4.4
1 | |
运行结果
1 | |
4.2
1 | |
结果
1 | |


